AIML - CNN基础知识

• AIML - CNN基础知识
  • CNN基础知识
    • CNN 卷积神经网络
    • Convolution 卷积
    • Padding 填充
      • valid padding
      • same padding
    • Stride 步长
    • 多通道卷积
    • Mask
      • 深度学习中的mask
      • 为什么需要 Mask
      • Mask 为解决 PAD 问题顺应而生
      • 常见的 Mask
        • Padding mask
        • Sequence mask

---

AIML - CNN基础知识

---

CNN基础知识

---

CNN 卷积神经网络

• 卷积神经网络 （convolutional neural network，CNN）是指至少在网络的一层中 使用卷积运算来代替一般的矩阵乘法运算 的神经网络，因此命名为卷积神经网络. [^CNN基础知识]

---

Convolution 卷积

我们以灰度图像为例进行讲解：

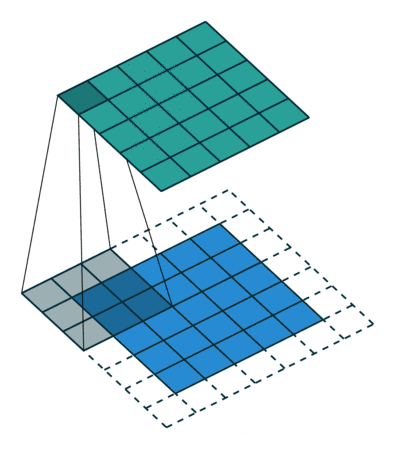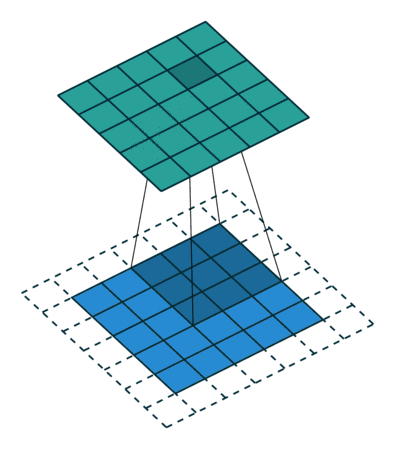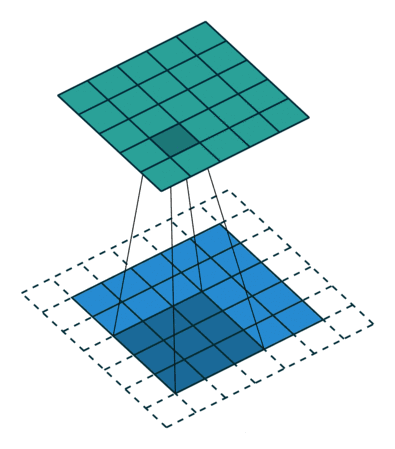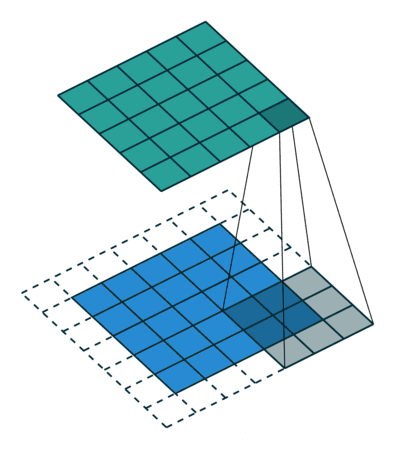
• 从一个小小的权重矩阵，也就是卷积核（kernel）开始，让它逐步在二维输入数据上“扫描”。
• 卷积核“滑动”的同时，计算权重矩阵和扫描所得的数据矩阵的乘积，然后把结果汇总成一个输出像素。

深度学习里面所谓的卷积运算，其实它被称为 互相关（cross-correlation）运算：

• 将图像矩阵中，从左到右，由上到下，取与滤波器同等大小的一部分
• 每一部分中的值与滤波器中的值对应相乘后求和，最后的结果组成一个矩阵，其中没有对核进行翻转。

一般卷積網路過程中，除了Input image不稱為Feature map外，中間產生的圖我們都稱之為Feature map

• 原因很簡單就是這些中間產生的圖都是為了「描繪出該任務所應該產生對應的特徵資料」
• 也呼應Yann LeCun, Yoshua Bengio & Geoffrey Hinton寫的Deep Learning第一句話寫的「Deep learning allows computational models that are composed of multiple processing layers to learn representations of data with multiple levels of abstraction」
• 深度學習過程就是在學資料的特性，所以中間出來的結果都是特徵資料，在影像因為是2D，所以用Feature map來稱呼。[^卷積計算中的步伐和填充]

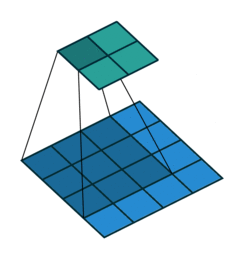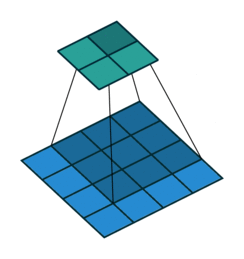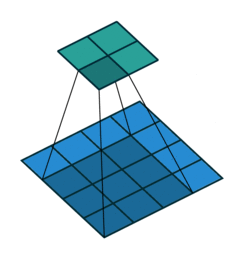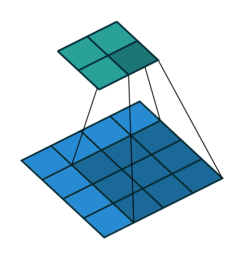
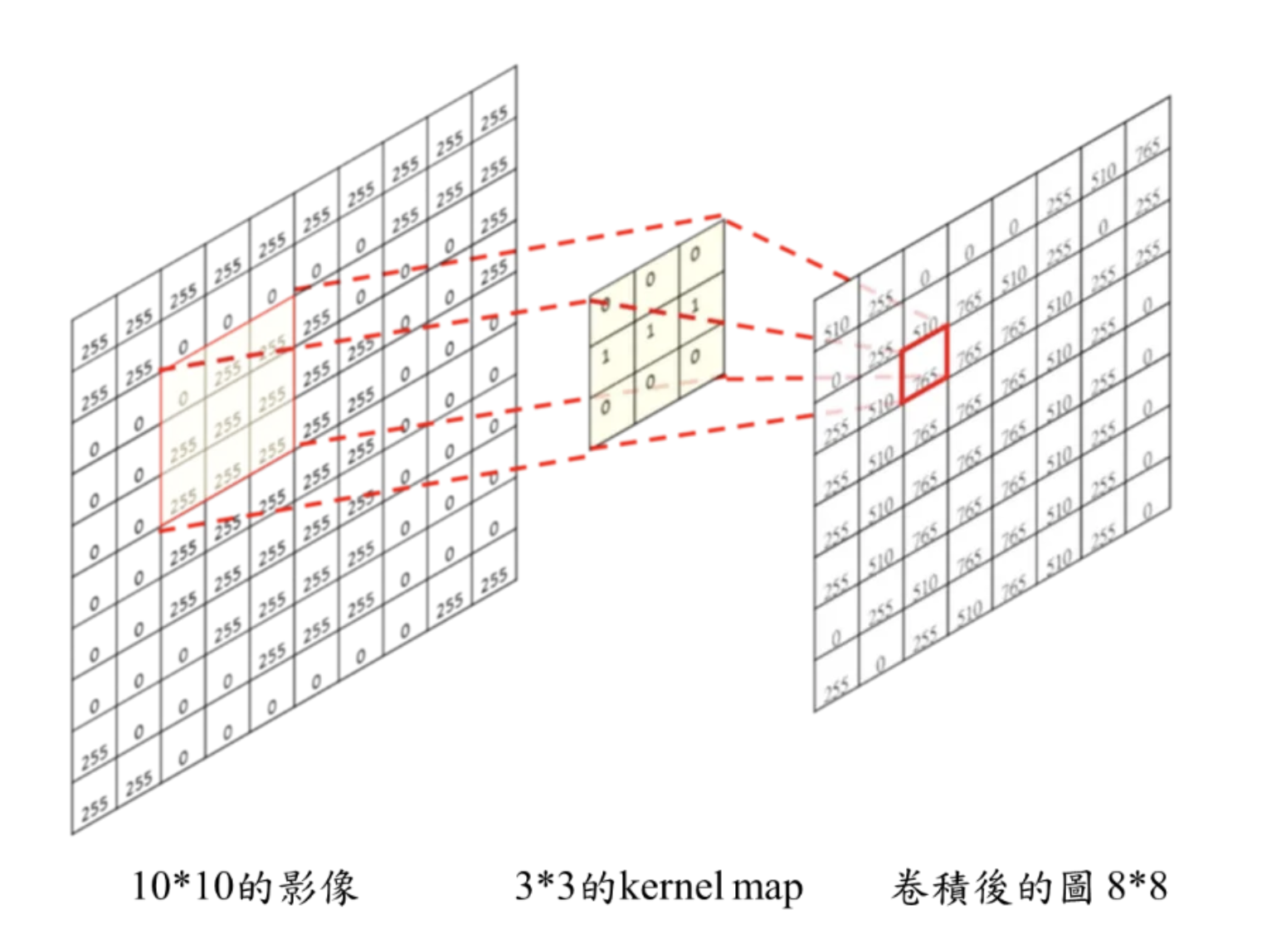
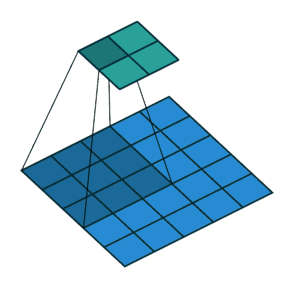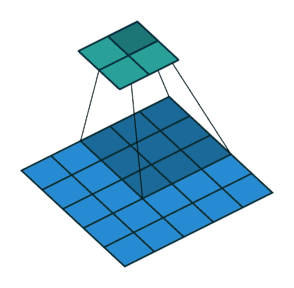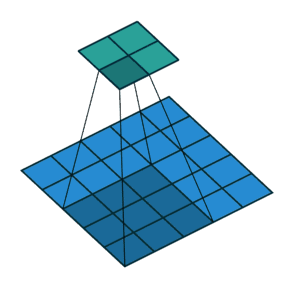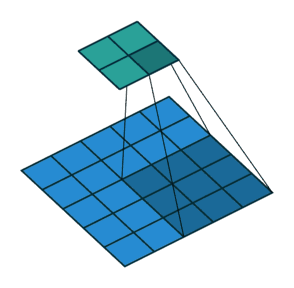
一個卷積計算基本上有幾個部份:

1. 輸入的圖: 假設大小是 $W × W$。
2. Filter (kernel map)大小是 $ks × ks$
3. Stride: kernel map在移動時的步伐長度 $S$
4. 輸出的圖大小為 $new_height × new_width$

例子:

1. 輸入的圖: W × W =10 × 10。
2. Filter (kernel map): ks × ks=3 × 3
3. Stride: S=1
4. 輸出的圖大小為 new_height × new_width = 8 × 8
   • 

卷積計算部份除了基本的input和filter (kernel map)通常還有兩個參數可以調(strides, padding)

---

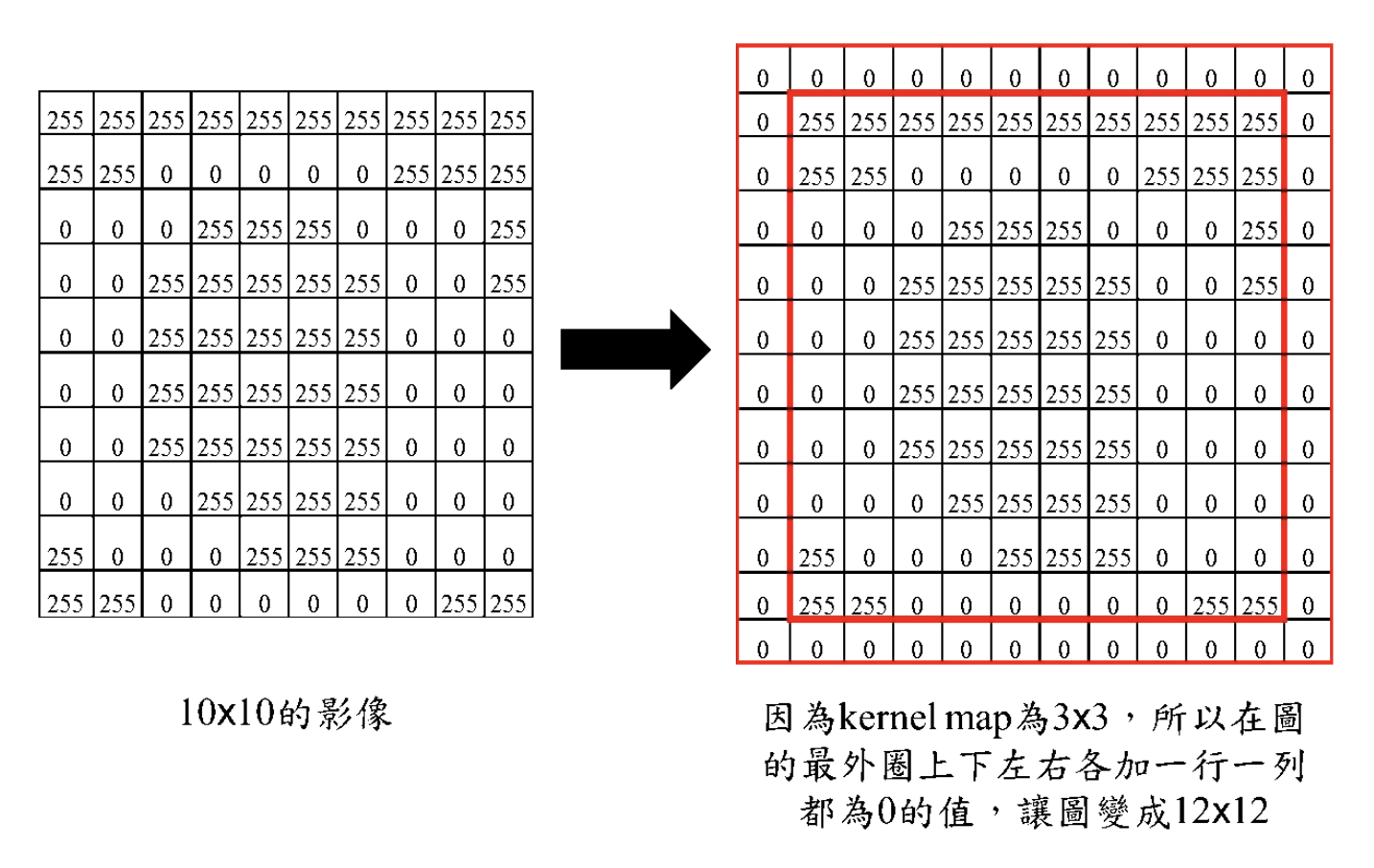
Padding 填充

输入图像与卷积核进行卷积后的结果中损失了部分值，输入图像的边缘被“修剪”掉了

• （边缘处只检测了部分像素点，丢失了图片边界处的众多信息）。
• 这是因为边缘上的像素永远不会位于卷积核中心，而卷积核也没法扩展到边缘区域以外。

这个结果我们是不能接受的

• 有时我们还希望输入和输出的大小应该保持一致。
• 为解决这个问题，可以在进行卷积操作前，对原矩阵进行边界 填充（Padding） ，也就是在矩阵的边界上填充一些值，以增加矩阵的大小，通常都用“ 0 ”来进行填充的。
• 通过填充的方法，当卷积核扫描输入数据时，它能延伸到边缘以外的伪像素，从而使输出和输入size相同。

常用的两种padding：

1. valid padding
2. same padding / zero padding

在tensorflow，padding那邊給了兩個選項「padding = ‘VALID’」和「padding = ‘SAME’」

valid padding

• 不进行任何处理，只使用原始图像，不允许卷积核超出原始图像边界
• padding = ‘VALID’ 等於最一開始敘述的卷積計算，圖根據filter大小和stride大小而變小。

same padding

• 进行填充，允许卷积核超出原始图像边界，并使得卷积后结果的大小与原来的一致

• padding = ‘SAME’，會用zero-padding的手法，讓輸入的圖不會受到kernel map的大小影響。

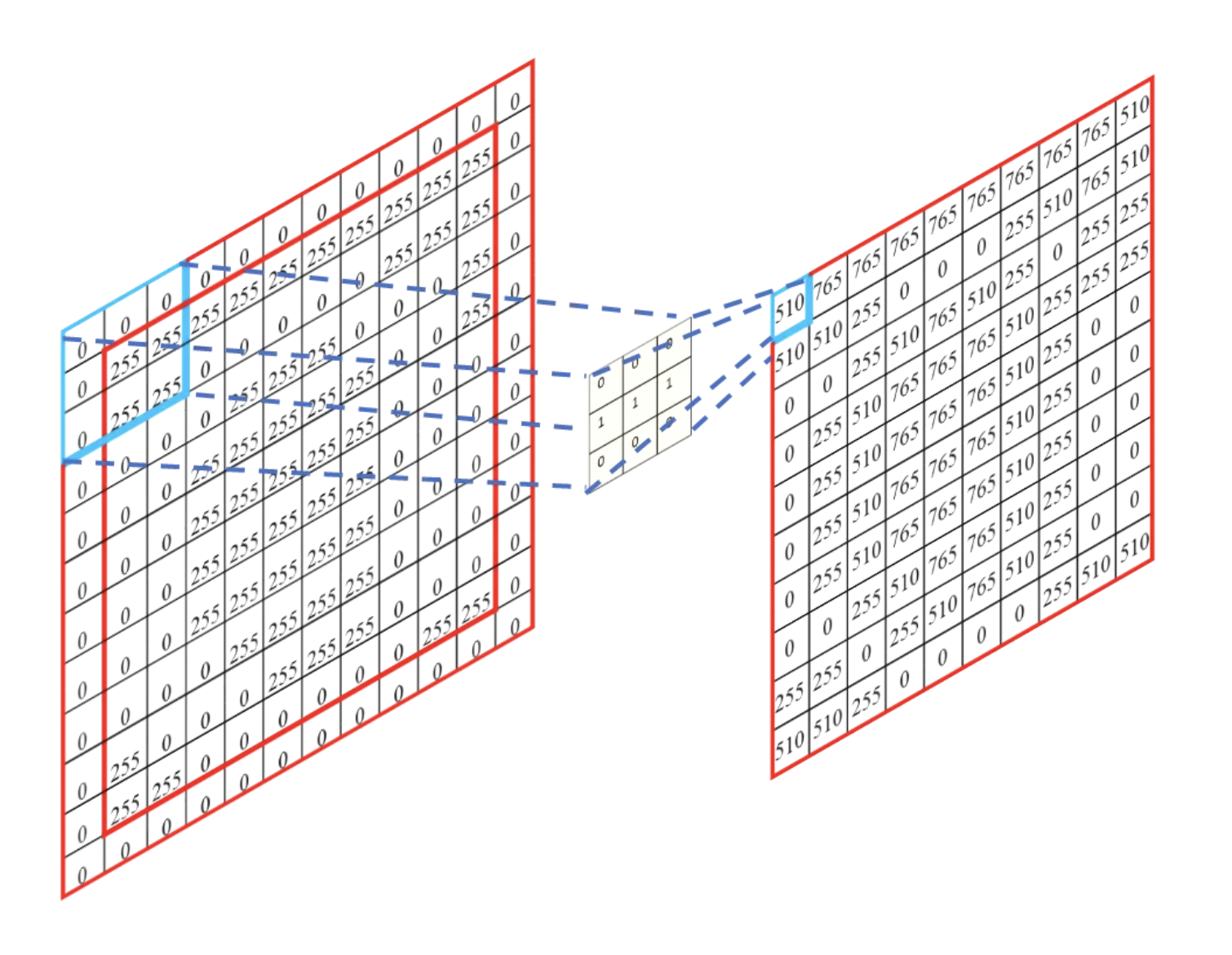
zero padding

• 看你會消失多少的大小，在輸入的圖部份就給你加上0元素進去
• 此刻的卷積計算如下，這樣卷積後的圖就不會變小了。

---

Stride 步长

• 滑动卷积核时，我们会先从输入的左上角开始，每次往左滑动一列或者往下滑动一行逐一计算输出，我们将每次滑动的行数和列数称为Stride
  • 在之前的图片中，Stride=1；在下图中，Stride=2。
  • 

卷积过程中，有时需要通过padding来避免信息损失，有时也要在卷积时通过设置的 步长（Stride） 来压缩一部分信息，或者使输出的尺寸小于输入的尺寸。

Stride的作用：

• 是成倍缩小尺寸，而这个参数的值就是缩小的具体倍数，比如
  • 步幅为2，输出就是输入的1/2
  • 步幅为3，输出就是输入的1/3

卷积核的大小一般为奇数\奇数

• 1\1，3\3，5\5，7\7 都是最常见的。
• 没有偶数\偶数
  • 更容易padding
    • 在卷积时，我们有时候需要卷积前后的尺寸不变。
    • 这时候我们就需要用到padding。
    • 假设图像的大小，也就是被卷积对象的大小为n\n，卷积核大小为k\k，padding的幅度设为(k-1)/2时，卷积后的输出就为(n-k+2((k-1)/2))/1+1=n，即卷积输出为n\n，保证了卷积前后尺寸不变。
    • 但是如果k是偶数的话，(k-1)/2就不是整数了。
  • 更容易找到卷积锚点
    • 在CNN中，进行卷积操作时一般会以卷积核模块的一个位置为基准进行滑动，这个基准通常就是卷积核模块的中心。
    • 如果卷积核为奇数，卷积锚点很好找，自然就是卷积模块中心
    • 如果卷积核是偶数，这时候就没有办法确定了，让谁是锚点似乎都不怎么好。

卷积的计算公式

• 输入图片的尺寸： 一般用 $n\times$ 表示输入的image大小。
• 卷积核的大小： 一般用 $f\times$ 表示卷积核的大小。
• 填充（Padding）： 一般用 $p$ 来表示填充大小。
• 步长(Stride)： 一般用 $s$ 来表示步长大小。

• 输出图片的尺寸： 一般用 $o$ 来表示。

• 如果已知 $n 、 f 、 p 、 s$ 可以求得 $o$ , 计算公式如下:
  • $o=\lfloor \frac{n + 2p - f}{s} \rfloor + 1$

其中” $\lfloor \ \rfloor$ “是向下取整符号，用于结果不是整数时进行向下取整。

---

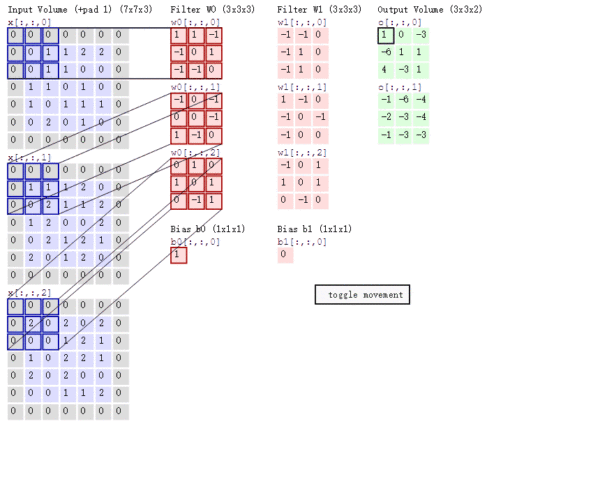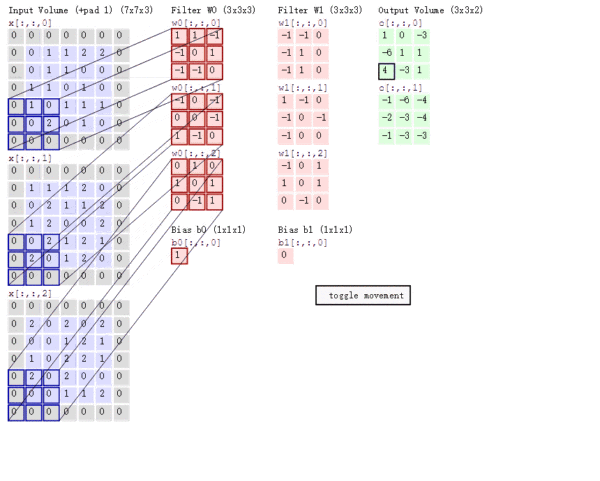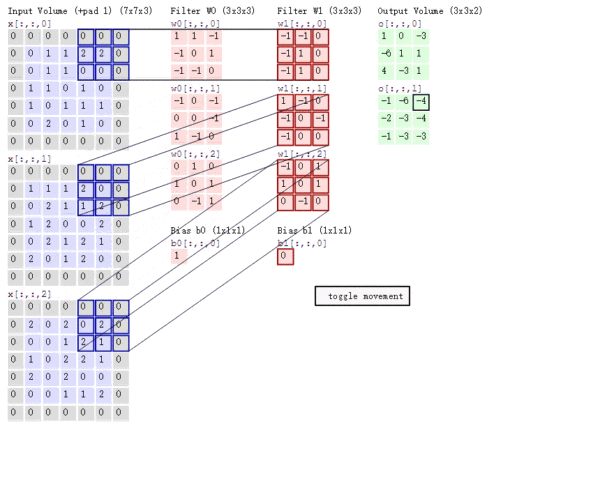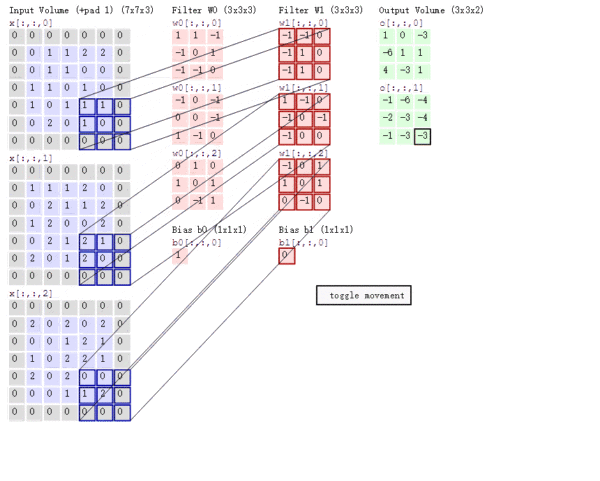
多通道卷积

上述例子都只包含一个输入通道。实际上，大多数输入图像都有 RGB 3个通道。

这里就要涉及到“卷积核”和“filter”这两个术语的区别。

• 在只有一个通道的情况下，“卷积核”就相当于“filter”，这两个概念是可以互换的。
• 但在一般情况下，它们是两个完全不同的概念。
• 每个“filter”实际上恰好是“卷积核”的一个集合 ，在当前层，每个通道都对应一个卷积核，且这个卷积核是独一无二的。

多通道卷积的计算过程：

• 将矩阵与滤波器对应的每一个通道进行卷积运算，最后相加，形成一个单通道输出，加上偏置项后，我们得到了一个最终的单通道输出。
• 如果存在多个filter，这时我们可以把这些最终的单通道输出组合成一个总输出。

还需要注意一些问题

• 滤波器的通道数、输出特征图的通道数。
• 某一层滤波器的通道数 = 上一层特征图的通道数。
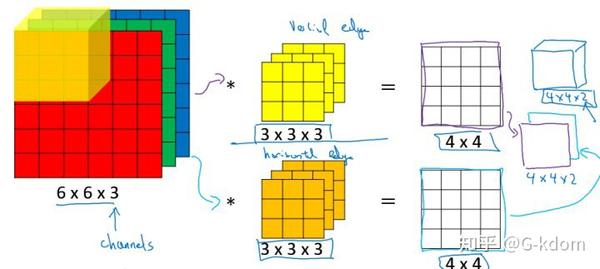
  • 输入一张 $6\times6\times3$ 的RGB图片，
  • 那么滤波器（ $3\times3\times3$ ）也要有三个通道。
• 某一层输出特征图的通道数 = 当前层滤波器的个数。
  • 当只有一个filter时，输出特征图（ $4\times4$ ）的通道数为1；
  • 当有2个filter时，输出特征图（ $4\times4\times2$ ）的通道数为2。

---

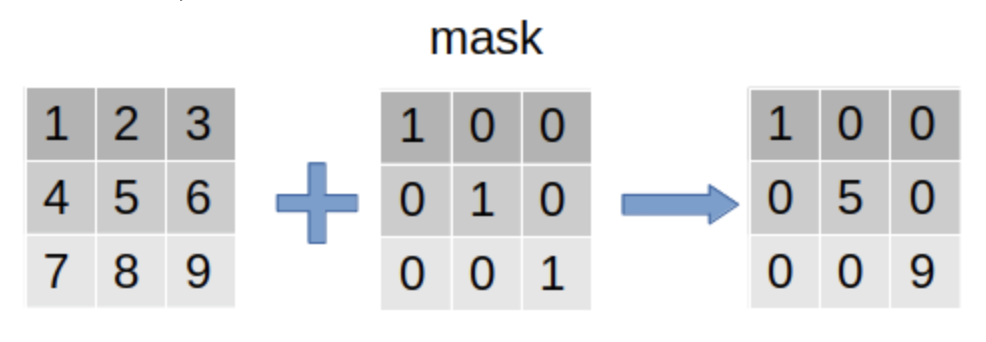
Mask

深度学习中的mask

• 分类的结果叫label。

• 分割的结果叫mask。

• 因为分割结果通常会半透明的覆盖在待分割目标上，所以就叫它掩膜吧。[^深度学习中的mask]

所谓 Mask，更像是语义分割的概念。

• 例子，看看下图，把它分为三个要素，竹子，熊猫，天空，也就是三个类别，分别记为，-1，0，1
• 我们现在可以构建一个Mask矩阵A，大小也图片包含的像素数量相同，初始值设为0，
• 所有分类为竹子的像素所在位置的值设为-1，为熊猫设为0，为天空的设为1
• 那么这个矩阵就变成了一个 Mask 矩阵，因为它可以把属于不同语义的像素分割出来。
• 在Mask-RCNN中的应用和这也差不多，只不过放在了最后的步骤。

为什么需要 Mask

需要mask的最重要的原因之一是, 要batchize多个句子作为一个输入，即输入了一批句子的模型做一个向前计算。

像这样的成像案例：

• 两个句子：

I like cats.
He does not like cats.

• 然后我们通过词汇表中的索引将每个单词转换为int：

1I 2He 3like 4does 5not 6cats…。

1 3 6 0
2 4 5 3 6 0

• 如果要将这两个句子作为一个批处理连接到网络（在Pytorch，tensorflow中使用其他方法），则需要将它们作为张量或矩阵。
• 但是它们的长度不同。所以给它们填充一些随机整数：

1 3 6 0 9 9

2 4 5 3 6 0

• 现在它变成了2x6矩阵。
• 然后您可以将此矩阵提供给网络。
• 但是这些填充物是没有意义的，甚至是有害的。因此，您需要提供有关蒙版填充的模型信息

1 1 1 1 0 0

1 1 1 1 1 1

• 因此，在计算时，模型可以使用mask过滤掉填充（第一句末尾为9 9）。

• 在 NLP 中，一个最常见的问题便是输入序列长度不等，通常需要进行 PAD 操作，通常在较短的序列后面填充 0

• 虽然 RNN 等模型可以处理不定长输入，但在实践中，需要对 input 做 batchsize，转换成固定的 tensor。

• PAD 案例：

  • 如下是两句英文，先将文本转换成数字

    s1 = 'He likes cats'
    s2 = 'He does not like cats'
    s = s1.split(' ') + s2.split(' ')
    
    word_to_id = dict(zip(s, range(len(s))))
    id_to_word = dict((k,v) for v,k in word_to_id.items())
    # {'He': 3, 'likes': 1, 'cats': 7, 'does': 4, 'not': 5, 'like': 6}
    # {3: 'He', 1: 'likes', 7: 'cats', 4: 'does', 5: 'not', 6: 'like'}
    
    s1_vector = [word_to_id[x] for x in s1.split(' ')]
    s2_vector = [word_to_id[x] for x in s2.split(' ')]
    sentBatch = [s1_vector, s2_vector]
    print(sentBatch)
    

  • 对文本进行数字编码

    [[3, 1, 7], [3, 4, 5, 6, 7]]
    

  • 对如上两个 vector 进行 pad 处理。

    from torch.nn.utils.rnn import pad_sequence
    a = torch.tensor(s1_vector)
    b = torch.tensor(s2_vector)
    pad = pad_sequence([a, b])
    print(pad)
    

  • PAD 结果

    tensor([[3, 3],
            [1, 4],
            [7, 5],
            [0, 6],
            [0, 7]])
    

以句子 ”He likes cats“ 的 PAD 结果举例：[3, 1, 7, 0, 0]，PAD 操作会引起以下几个问题。

1. mean-pooling 的问题

• 如上述案例所示，对于矩阵： $s1 = [3, 1, 7]$

• 对 s1 进行 mean-pooling： $mean_{s1}=(3+1+7)/3=3.667$

• 进行 pad 之后： $pad_{s1}=[3,1,7,0,0]$

• 对 $pad_{s1}$ 进行 mean-pooling： $pad_{s1}=(3+1+7+0+0)/10=1.1$

• 对比 $mean_{s1}$ 和 $pad_{s1}$ 发现：pad 操作影响 mean-pooling。

2. max-pooling 的问题

• 对于矩阵 s1: $s1 = [-3, -1, -7]$ ，PAD 之后： $pad_{s1}=[-3,-1,-7,0,0]$

• 分别对 s1 和 $pad_{s1}$ 进行 max-pooling： $max_{s1}=-1, max_{pad_{s1}}=0$

• 对比 $mean_{s1}$ 和 $pad_{s1}$ 发现：pad 操作影响 max-pooling。

3. attention 的问题

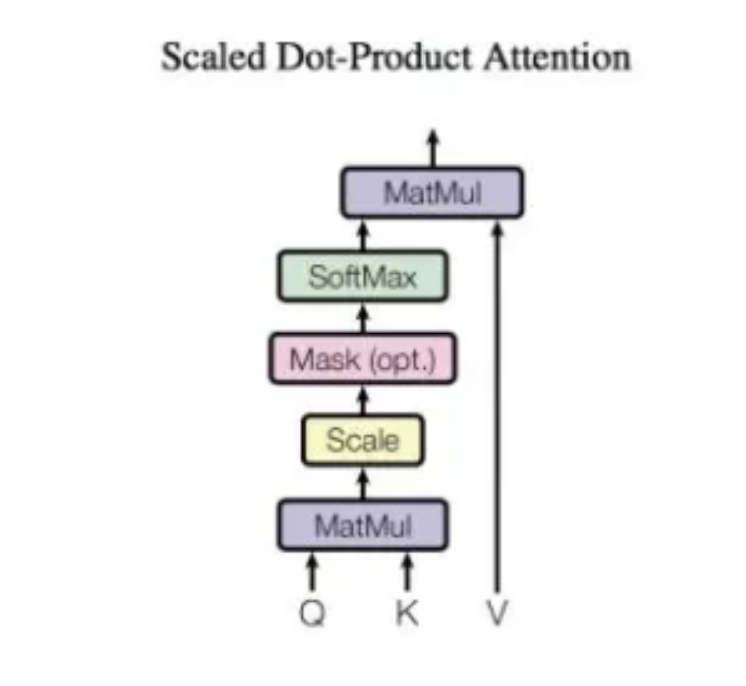
• 通常在 Attention 计算中最后一步是使用 softmax 进行归一化操作，将数值转换成概率。
• 但如果直接对 PAD 之后的向量进行 softmax，那么 PAD 的部分也会分摊一部分概率，这就导致有意义的部分 (非 PAD 部分) 概率之和小于等于 1。

---

Mask 为解决 PAD 问题顺应而生

Mask 是相对于 PAD 而产生的技术，具备告诉模型一个向量有多长的功效。

Mask 矩阵有如下特点：

1. Mask 矩阵是与 PAD 之后的矩阵具有相同的 shape。
2. mask 矩阵只有 1 和 0两个值，如果值为 1 表示 PAD 矩阵中该位置的值有意义，值为 0 则表示对应 PAD 矩阵中该位置的值无意义。

在第一部分中两个矩阵的 mask 矩阵如下所示：

mask_s1 = [1, 1, 1, 0, 0]
mask_s2 = [1, 1, 1, 1, 1]
mask = a.ne(torch.tensor(paddingIdx)).byte()
print(mask)
>>> tensor([[1, 1],
            [1, 1],
            [1, 1],
            [0, 1],
            [0, 1]], dtype=torch.uint8)

1. 解决 mean-pooling 问题

$mean_s1=sum(pad_{s1}\m)/sum(m)$

2. 解决 max-pooling 问题

在进行 max-pooling 时，只需要将 pad 的部分的值足够小即可，可以将 mask 矩阵中的值为 0 的位置替换的足够小 ( 如: $10^{-10}$ 甚至 负无穷 ，则不会影响 max-pooling 计算。

$max_b=max(pad_b-(1-m)\10^{-10})$

3. 解决 Attention 问题

该问题的解决方式跟 max-pooling 一样，就是将 pad 的部分足够小，使得 $e^x$ 的值非常接近于 0，以至于忽略。

$softmax(x)=softmax(x-(1-m)\10^{10})$

---

常见的 Mask

在Transformer模型中，mask的作用是控制模型在处理序列时对未来信息的可见性。

• Transformer模型是一个自注意力机制的序列到序列模型，它通过将输入序列中的每个位置与其他位置进行交互来建模上下文关系。
• 当我们预测目标序列的下一个位置时，为了避免模型能够”看到”未来信息，需要使用mask将未来位置的信息屏蔽掉。

具体来说，在Transformer中有两种常用的mask方式：padding mask和look-ahead mask。

1. Padding mask
   1. 用于处理不定长输入
   2. 在输入序列中，可能存在不等长的句子，为了保持输入序列的统一长度，我们会在较短的句子后面添加一些特殊符号（如0）进行填充。
   3. Padding mask就是用来标记这些填充位置，在计算注意力权重时，将填充位置的注意力权重设为一个很小的值（如负无穷），使得模型不会关注这些填充位置。
2. Look-ahead mask / seqence-mask
   1. 在Transformer的解码器中，为了生成目标序列的下一个位置时只使用已经生成的部分序列，会使用look-ahead mask。
   2. Look-ahead mask将当前位置之后的位置都屏蔽掉，确保模型只能看到当前位置之前的信息，避免了信息泄露。

通过使用这些mask，Transformer能够更好地处理不等长序列，并且在生成目标序列时不会依赖未来信息，提高了模型的性能和泛化能力。

• 在 NLP 任务中，因为功能不同，Mask 也会不同。

---

Padding mask

在 NLP 中，一个常见的问题是输入序列长度不等

• 在处理序列数据时，由于不同的序列可能具有不同的长度，我们经常需要对较短的序列进行填充（padding）以使它们具有相同的长度。对一个 batch 内的句子进行 PAD，通常值为 0。
  • PAD 为 0 会引起很多问题，影响最后的结果，
  • 在模型的计算过程中，这些填充值是没有实际意义的
• 因此我们需要一种方法来确保模型在其计算中忽略这些填充值。这就是padding mask的作用。

比如常用的就是在数据集准备中，想用batch来训练，就得将一个batch的数据的长度全部对齐。

Padding mask

• 是一个与输入序列形状相同的二进制矩阵，用于指示哪些位置是真实的数据，哪些位置是填充值。

• 真实数据位置的mask值为0。填充位置的mask值为1。

• 用处：[^对transformer使用PaddingMask]

  • 忽略无关信息：通过使用padding mask，我们可以确保模型在其计算中忽略填充值，从而避免这些无关的信息对模型的输出产生影响。

  • 稳定性：如果不使用padding mask，填充值可能会对模型的输出产生不稳定的影响，尤其是在使用softmax函数时。

  • 解释性：使用padding mask可以提高模型的解释性，因为我们可以确保模型的输出只与真实的输入数据有关，而不是与填充值有关。

  • padding mask是处理序列数据时的一个重要工具，它确保模型在其计算中忽略填充值，从而提高模型的性能和稳定性。

使用Padding Mask:

• 在自注意力机制中，我们计算查询和键的点积来得到注意力分数。
• 在应用softmax函数之前，我们可以使用padding mask来确保填充位置的注意力分数为一个非常大的负数（例如，乘以-1e9）。
• 这样，当应用softmax函数时，这些位置的权重将接近于零，从而确保模型在其计算中忽略这些填充值。

例子：

1. case 1

case 1: I like cats.
case 2: He does not like cats.

# 假设默认的 seq_len 是5
# 一般会对 case 1 做 pad 处理，变成
[1, 1, 1, 0, 1]

# - 在上述例子数字编码后，开始做 embedding，而 pad 也会有 embedding 向量，但 pad 本身没有实际意义，参与训练可能还是有害的。
# - 因此，有必要维护一个 mask tensor 来记录哪些是真实的 value
# 上述例子的两个 mask 如下：
1 1 1 0 0
1 1 1 1 1
# - 后续再梯度传播中，mask 起到了过滤的作用，在 pytorch 中，有参数可以设置：
nn.Embedding(vocab_size, embed_dim, padding_idx=0)

1. 假设我们有一个长度为4的序列：[A, B, C,]，其中是填充标记。对应的padding mask是：[0, 0, 0, 1]。

# 在计算注意力分数后，使用以下方法应用padding mask：
attention_scores = attention_scores.masked_fill(mask == 1, -1e9)
# 这里，masked_fill是一个PyTorch函数，它会将mask中值为1的位置替换为-1e9

• 这里的attention_scores就是 $Q×K$ 的矩阵，把尾部多余的部分变成-inf，再过SoftMax，这样就是0了。
• 这样，即使V的后半部分有padding的部分，也会因为乘0而变回0。
• 这样被padding掉的部分就从计算图上被剥离了，由此不会影响模型的训练。

import torch.nn as nn

class Attention(nn.Module):
    def __init__(self, dim, num_heads=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0.):
        super().__init__()
        self.num_heads = num_heads
        head_dim = dim // num_heads
        self.scale = qk_scale or head_dim ** -0.5
        self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop)
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop)

    def forward(self, x, mask=None):
        B, N, C = x.shape
        qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
        q, k, v = qkv[0], qkv[1], qkv[2]

        attn = (q @ k.transpose(-2, -1)) * self.scale

        # Apply the padding mask
        if mask is not None:
            attn = attn.masked_fill(mask.unsqueeze(1).unsqueeze(2) == 1, float('-inf'))

        attn = attn.softmax(dim=-1)
        attn = self.attn_drop(attn)

        x = (attn @ v).transpose(1, 2).reshape(B, N, C)
        x = self.proj(x)
        x = self.proj_drop(x)
        return x

---

Sequence mask

• 在语言模型中，常常需要从上一个词预测下一个词，sequence mask 是为了使得 decoder 不能看见未来的信息。
• 也就是对于一个序列，在 time_step 为 t 的时刻，我们的解码输出应该只能依赖于 t 时刻之前的输出，而不能依赖 t 之后的输出。
• 因此我们需要想一个办法，把 t 之后的信息给隐藏起来。

具体怎么做

• 产生一个上三角矩阵，上三角的值全为 1，下三角的值全为 0，对角线也是 0 。
• 把这个矩阵作用在每一个序列上，就可以达到目的

一个常见的 trick 就是生成一个 mask 对角矩阵:

def sequence_mask(seq):
    batch_size, seq_len = seq.size()
    mask = torch.triu(torch.ones((seq_len, seq_len), dtype=torch.uint8), diagonal=1)
    mask = mask.unsqueeze(0).expand(batch_size, -1, -1)  # [B, L, L]
    return mask